こよみ用語解説

天体の地心座標

視赤経 (しせきけい)、視赤緯 (しせきい)、視黄経 (しこうけい)、視黄緯 (しこうい)

瞬時の真春分点と真赤道にもとづく座標系における値で、光行差を含みます。

地心距離 (ちしんきょり)

地心距離は天文単位 (au，1 au = 149,597,870.7 km) で表した地球からの真距離です。ただし，月の距離は月と地球との平均距離 (384,400 km) を単位とした値です。オプションでkm単位を選択することもできます。

視差 (しさ)

視差は赤道地平視差πで，sin π＝(地球の赤道半径)／(地球・天体間の距離)、となります。

視半径 (しはんけい)

一般に、天体の視半径sは、sin s＝(天体の赤道半径または極半径)／(地球・天体間の距離)、で表わせます。太陽については、距離が1天文単位のときの値を16′1.18″として算出したものとあわせて表示しています。

天文測定位置 (てんもんそくていいち)

準惑星や小惑星のような暗い太陽系天体については、星表や星図と直接比較できるよう、国際天文基準座標系における天文測定位置を掲載しています。

また、これらの天体の等級については、1985年のIAU総会 (Commission 20) で採択されたH-G等級システムを採用しています。

天体の日心座標

日心黄経 (にっしんこうけい)、日心黄緯 (にっしんこうい)

瞬時の平均春分点と黄道にもとづく座標系における値で、光行差は含みません。

動径 (どうけい)

動径は天文単位 (au，1 au = 149,597,870.7 km) で表した太陽からの真距離です。

軌道経度 (きどうけいど)、日変化

軌道経度は春分点から黄道に沿ってその天体の昇交点まで測り、さらにそこから軌道上を天体の位置まで測った値、すなわち昇交点黄経と近日点引数の和です。日変化は軌道経度の1日あたりの変化量です。

太陽の自転軸

太陽の自転

太陽面上に現われる黒点が毎日動いていく様子から、太陽はある方向の直線を軸として自転していることがわかります。自転軸の方向はおよそ赤経19^h5^m、赤緯+63.9°です。地球に対する自転の周期は27.2753日、恒星に対する周期は25.38日になります (カリントン周期：日面緯度±16°付近)。

自転軸の位置

「太陽の自転軸」ではP, B₀, L₀を用いて表現されます。Pは地球から見た自転軸の向きで、自転軸の北側が天球の北より東に傾いているものを＋、西に傾いているものを−としています。B₀、L₀は地球から見た太陽面の中点の日面緯度および日面経度で、日面経度は1854年1月1日グリニジ平均正午において黄道面に対する太陽の赤道面の昇交点を通る日面子午線を経度の原点としたものです。P、B₀の値は4年ごとにだいたい同じになります。

月の自転軸

自転軸の位置

Pは地球から見た自転軸の向きで、自転軸の北側が天球の北より東に傾いているものを＋、西に傾いているものを−としています。

B₀、L₀は地球から見た月面の中点の月面緯度および月面経度です。月面の座標系は平均地球・極の方向にもとづいています (mean Earth/polar axis system, ME system)。

太陽の位置

Bs、Lsは太陽から見た月面の中点Xsの月面緯度および月面経度です。Psは地球から見たXsの向きで、天球の北より東に傾いているものを＋、西に傾いているものを−としています。

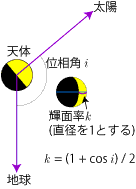i は太陽-月-地球のなす角で、位相角といいます。k は月の直径のうち太陽に照らされる部分の占める割合で、輝面率といいます。これらは k = (1 + cos i) / 2 という関係にあり、i = 0°では k = 1、i = 180°では k = 0 となります。

ただし、月の公転軌道は黄道に対して傾きを持つので、そのような値になることは基本的にありませんし、近い値になれば、それぞれ月食・日食となってしまいます。

惑星の自転軸

自転軸の位置

Pは地球から見た自転軸の向きで、自転軸の北側が天球の北より東に傾いているものを＋、西に傾いているものを−としています。なお、惑星の自転軸は太陽系の不変面≒黄道面に対して地球の北極と同じ側にあるほうを北側としています。

B₀、L₀は地球から見た惑星面の中点の惑星面緯度および惑星面経度です。惑星面緯度は惑星の扁平率を考慮しています。惑星面経度は惑星の自転によって経度が増えていく方向に、水星はHun Kalクレーターを経度20°として、金星はAriadneクレーターの中央丘を経度0°として、火星はAiry-0クレーターを経度0°として (厳密にはバイキング1号着陸機の経度を西経47.95137°として)、木星・土星・天王星は磁場〜体系IIIを基準として、海王星は大気中の模様〜体系IIを基準として測ります。

太陽の位置

Bs、Lsは太陽から見た惑星面の中点Xsの惑星面緯度および惑星面経度です。Psは地球から見たXsの向きで、天球の北より東に傾いているものを＋、西に傾いているものを−としています。

iは位相角、kは輝面率です (「月の自転軸」の図参照)。

λsは惑星の黄道における太陽黄経です。惑星の赤道面に対する惑星の黄道の昇交点〜惑星の春分点を基準として測ります。

グリニジ恒星時

視恒星時 (しこうせいじ)、平均恒星時 (へいきんこうせいじ)、分点均差 (ぶんてんきんさ)

それぞれ、真春分点、平均春分点に対する恒星時の値です。分点均差は赤経における章動であり、視恒星時＝平均恒星時＋分点均差という関係が成り立ちます。

均時差 (きんじさ)

均時差＝視太陽の時角−平均太陽の時角です。

ユリウス日

ユリウス日

ユリウス日は−4712年1月1日から数えた通日です。「年月日→ユリウス日」、「ユリウス日→年月日」では紀元元年の前年を0年としているため、これを紀元前1年とする方法とは1年ずつの差異があります。たとえば−4712年は紀元前4713年となります。ユリウス日に小数をつけて時刻を示す場合には世界時より12時間＝0.5日遅れたグリニジ平均天文時に相当する値を用います。

ユリウス暦とグレゴリオ暦

季節は、春分点に対して地球が太陽の周りを公転する周期である1太陽年≒365.2422日で繰り返します。1年＝365日では0.2422日だけ不足するため、4年に1回、4で割り切れる年をうるう年として1日増やし、1太陽年に近づけるようにしたのがユリウス暦です。

しかし、4年に1回のうるう年では逆に0.2422 x 4 - 1 ≒ -0.03日 / 4年だけ補正しすぎることになりますから、100で割り切れて400で割り切れない年はうるう年にしないことにしました。これをグレゴリオ暦と呼び、現在もこれに従って日付が定められています。

時刻系

中央標準時 (ちゅうおうひょうじゅんじ)

日本国内で採用されている時刻系。中央標準時＝協定世界時＋9^h。日本標準時 (にほんひょうじゅんじ) ともいいます。

世界時 (せかいじ)

協定世界時＝世界時(UT1)−ΔUT1です。ΔUT1は観測により決まる量ですが、天体暦ではΔUT1＝0として推算します。このΔUT1が±0.9^s以内に収まるように、「うるう秒」による時刻調整が行なわれます。

地球時 (ちきゅうじ)

地心座標時の定数倍で、歩度が国際単位系の1^sとなるような時刻系です。以前の地球力学時に相当します。 地球時＝世界時(UT1)＋ΔＴという関係にあり、ΔＴは観測をもとに決定した推定値を用いています。